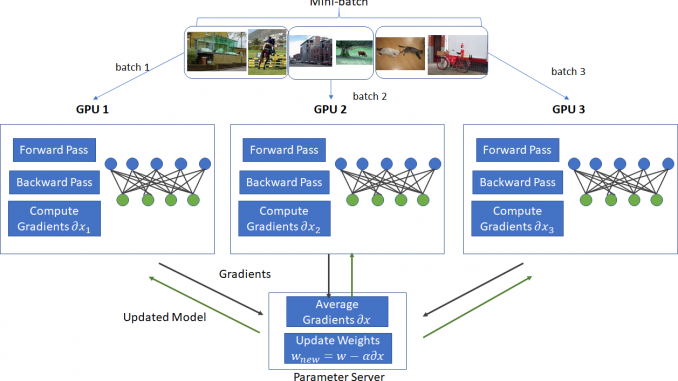
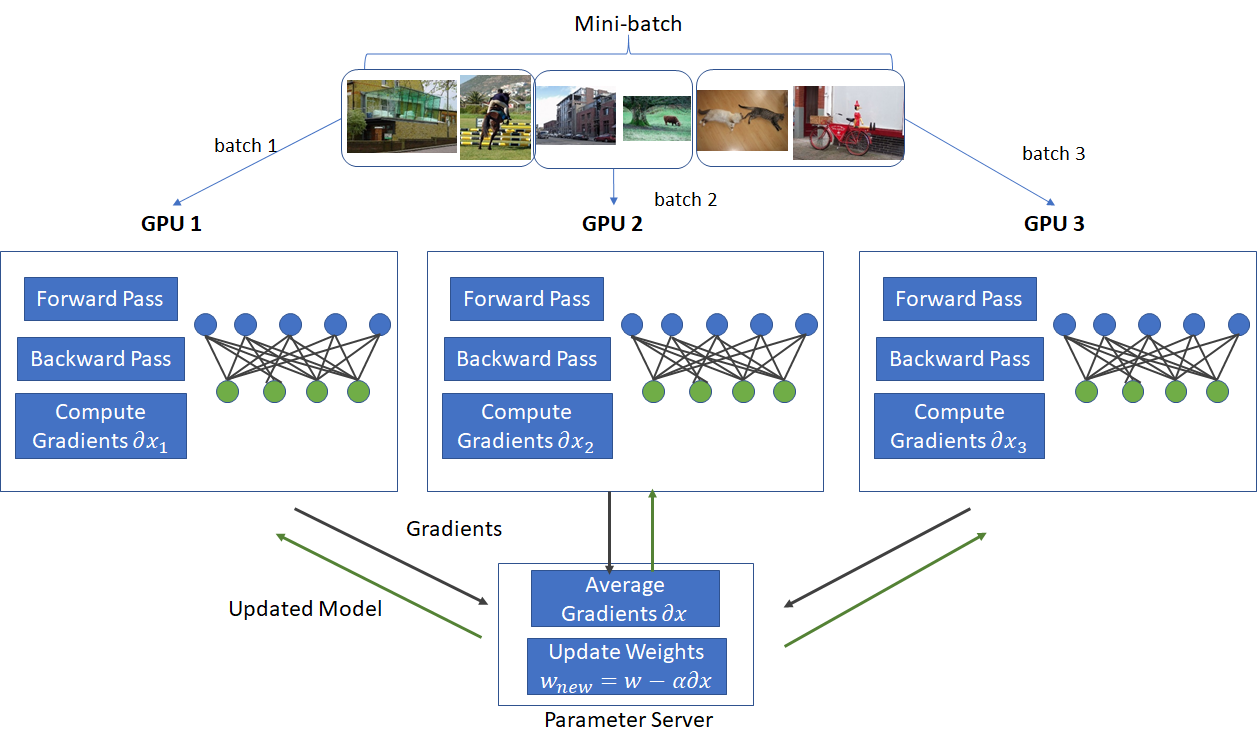
In this post, I’ll show how to modify the spiral data set example presented in Karpathy’s post (http://cs231n.github.io/neural-networks-case-study/) to run in a data parallel mode. Data parallelism is a popular technique used to speed up training on large mini-batches when each mini-batch is too large to fit on a GPU. Under data parallelism, a mini-batch is split up into smaller sized batches that are small enough to fit on the memory available on different GPUs on the network. Each GPU holds an identical copy of the network parameters and runs the forward and backward pass. At the end of the backward pass, each GPU sends the computed gradients to a parameter server. The parameter server aggregates the gradients and computes the updates to the network parameters using some variant of Stochastic Gradient Descent. The updated parameters are then sent to each GPU and the process is repeated for a fresh mini-batch. This process is shown in the diagram below.
Using data-parallelism and appropriately adjusting the learning rate, large number of GPUs can be used to process extremely large mini-batches (~8000 images) in parallel. For example, Girshick et al. (https://arxiv.org/pdf/1706.02677.pdf) show that with using a large minibatch size of 8192 on 256 GPUs, ResNet-50 can be trained on ImageNet in 1 hour while maintaining the same level of accuracy as the 256 minibatch baseline.
I decided to use the spiral dataset example as the neural network used to classify this dataset, while simple, still retains the essential elements of neural networks – two weight layers, a RELU activation layer and a softmax classifier. The example also demonstrates the effectiveness of neural networks in handling highly non-linear data. This ability arises from the use of RELU non-linearity in the activation layer. As shown here, removing the non-linearity will cause the classification accuracy to drop by almost half. I won’t go into the details of the network architecture as Karpathy’s post referenced above does an excellent job of describing the problem, the network architecture, calculation of gradients and details of the forward and backward steps. A movie showing how the decision boundaries adjust to the contours of the data as training progresses is shown below.
This post makes the following contributions:
- It shows how the training data can be split into two batches and the forward and backward steps for each batch can be executed on two “nodes” (a node represents a GPU in a real networked implementation)
- Shows the implementation of a “parameter server” that aggregates the gradients from the nodes and after gradients from all nodes have been received, computes the updates to the network parameters using a simplified stochastic gradient descent (with a constant learning rate and no momentum).
- Major data transfer operations (sending batch data to each node, gradients from the nodes to the parameter server and updated weights from the parameter server to each node) are split up into separate steps to make it easy to see exactly what and how much data is sent in each step
- Python threading APIs are used to execute each node on a separate thread. Since the amount of processing involved in this toy example is relatively small, threading doesn’t result in a significant speed up. However when each node is slowed down by inserting a sleep, the multi-threaded implementation takes half the time of the non-threaded implementation.
Without Multi-Threading
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
processing task: node1 finished processing task: node1 processing task: node2 finished processing task: node2 processing task: node1 finished processing task: node1 processing task: node2 finished processing task: node2 processing task: node1 finished processing task: node1 processing task: node2 finished processing task: node2 training time: 20.09 |
With Multi-Threading
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
processing task: node1 processing task: node2 finished processing task: node1 finished processing task: node2 processing task: node1 processing task: node2 finished processing task: node1 finished processing task: node2 processing task: node1 processing task: node2 finished processing task: node1 finished processing task: node2 training time: 10.07 |
The Code
I have written extensive comments in the code, so it should be easy to follow. To the best of my knowledge, I have also described more advanced techniques that are used in real systems that would have been an overkill here.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 |
import random import threading import numpy as np import matplotlib.pyplot as plt import queue import time N = 150 # number of points per class D = 2 # dimensionality (points are on 2D plane) K = 3 # number of classes X = np.zeros((N*K,D)) # data matrix (each row = single example) y = np.zeros(N*K, dtype='uint8') # class labels # We'll split up the data processing across two nodes. In the real world, these would be two hardware units such as GPUs. # In this example, each node will be executed on separate threads num_nodes = 2 # Code to generate spiral dataset for j in range(K): ix = range(N*j,N*(j+1)) r = np.linspace(0.0,1,N) # radius t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] y[ix] = j # lets visualize the data: plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral) plt.show() # initialize parameters randomly h = 100 # size of hidden layer W1 = 0.01 * np.random.randn(D, h) b1 = np.zeros((1, h)) W2 = 0.01 * np.random.randn(h, K) b2 = np.zeros((1, K)) # some hyperparameters step_size = 1e-0 reg = 1e-3 # regularization strength # The node class runs the forward and backward step of our network. class node(object): def __init__(self, W1, b1, W2, b2, ps, name): self.W1 = W1 self.W2 = W2 self.b1 = b1 self.b2 = b2 self.task_name = name self.dscores = [] self.ps = ps def data(self, X, y): self.X = X self.y = y self.batchSize = self.X.shape[0] # called by the parameter server when it has calculated updated weights def update(self, W1, b1, W2, b2): dW2_reg = reg * self.W2 dW1_reg = reg * self.W1 self.W1 = W1 self.W2 = W2 self.b1 = b1 self.b2 = b2 self.W2 += -step_size * dW2_reg self.W1 += -step_size * dW1_reg def forward_and_backward(self): self.forward() self.backward() def forward(self): # l1_i: layer 1 input # l1_o: layer 1 output # l1_ao: layer 1 activation output # l1_dw: layer 1 derivative of loss wrt layer weights # l1_db: layer 1 derivative of loss wrt layer bias # l1_delta: layer 1 derivative of loss wrt output self.l1_i = self.X self.l1_o = np.dot(self.l1_i, self.W1) + self.b1 self.l1_ao = np.maximum(0, self.l1_o) self.l2_i = self.l1_ao self.l2_o = np.dot(self.l2_i, self.W2) + self.b2 self.exp_scores = np.exp(self.l2_o) self.probs = self.exp_scores / np.sum(self.exp_scores, axis=1, keepdims=True) correct_logprobs = -np.log(self.probs[:, self.y]) self.data_loss = np.sum(correct_logprobs) self.data_loss = self.data_loss / self.batchSize self.dscores = self.probs self.dscores[np.arange(self.dscores.shape[0]), self.y] -= 1 self.dscores /= self.batchSize reg_loss = 0.5 * reg * np.sum(self.W1 * self.W1) + 0.5 * reg * np.sum(self.W2 * self.W2) self.loss = self.data_loss + reg_loss def backward(self): self.l2_dw = np.dot(self.l1_ao.T, self.dscores) self.l2_db = np.sum(self.dscores, axis=0, keepdims=True) # next backprop into layer 1 self.l1_a_delta = np.dot(self.dscores, self.W2.T); # through the activation layer self.l1_delta = self.l1_a_delta self.l1_delta[self.l1_ao <= 0] = 0 self.l1_dw = np.dot(self.l1_i.T, self.l1_delta) self.l1_db = np.sum(self.l1_delta, axis=0, keepdims=True) # send gradients to the parameter server. # In a real system, these updates would be sent over the network. # The amount of data being sent is the total size of the network weights. # Also note there are no dependencies between the gradients across layers. Thus, we don't have to wait until # all the gradients have been calculated to send them to the parameter server. Gradient transmission can be # pipelined with back-propagation, i.e., gradients for a layer can be sent to the parameter server right after # they are calculated. For big networks with a large number of parameters and/or slow network, doing so can result # in better resource utilization and improved efficiency. # This "pipelining" applies to the forward pass as well. Only the parameters for a given layer are needed to run the # forward pass for that layer. Thus, the transmission of updated parameter values from the parameter server can be # pipelined with the execution of the forward pass. self.ps.update_weights(self) # The parameter server class. This class defines methods to receive gradients from the nodes and averages the gradients # It then uses a constant learning rate to update the weights. A more sophisticated implementation would use a graduated # learning rate, momentum etc to update the weights. # The class also propagates the updated weights back to the nodes. # Note that for a real system consisting of multiple GPUs on several machines (for example, for training Resnet 50 on ImageNet, # the authors use 256 GPUs, 32 servers containing 8 GPUs each) sending each GPU's data to a centralized parameter server would # be quite expensive. More advanced networking techniques are used in such systems. For example the authors report using the # "halving/doubling" algorithm for inter-server reduce operations. class param_server(object): def __init__(self, W1, b1, W2, b2, y): self.W1 = W1 self.W2 = W2 self.b1 = b1 self.b2 = b2 self.y = y self.num_updates = 0 self.l2_dw = 0 self.l2_db = 0 self.l1_dw = 0 self.l1_db = 0 self.nodes = [] # accumulate gradients. Once gradients from all nodes have been received, compute the parameter updates and apply # those updates to the network parameters. Then propagate the parameters back to the nodes. def update_weights(self, node): self.num_updates += 1 # perform a parameter update self.l2_db += node.l2_db self.l2_dw += node.l2_dw self.l1_dw += node.l1_dw self.l1_db += node.l1_db self.nodes.append(node) if (self.num_updates == num_nodes): # we received gradients from all nodes, compute average and update the weights self.W2 += -step_size * self.l2_dw/num_nodes self.b2 += -step_size * self.l2_db/num_nodes self.W1 += -step_size * self.l1_dw/num_nodes self.b1 += -step_size * self.l1_db/num_nodes # In a real system, these updates would be sent over the network. The amount of data being # sent is the total size of the network. For example, VGG 19 has 144 Million Params, if each # parameter is represented as a 4 byte float, the total data sent (to each node) ~ 576 MB for node in self.nodes: node.update(self.W1, self.b1, self.W2, self.b2) # zero out accumulated gradients for next update cycle self.l2_db = 0 self.l2_dw = 0 self.l1_dw = 0 self.l1_db = 0 self.nodes = [] self.num_updates = 0 task_queue = queue.Queue() # This is the main task function that is executed by each thread. It pulls the latest node object from the task_queue and # executes the forward and backward step on it. At the end of the backward step, each node sends its gradients to the # parameter server. def forward_and_backward_pass(): while True: # task_queue.get will block if the queue is empty node = task_queue.get() # print("processing task: %s" % node.task_name) node.forward_and_backward() # print("finished processing task: %s" % node.task_name) task_queue.task_done() num_examples = X.shape[0] # number of samples in each batch B = (int)(num_examples/2) # Create the nodes and parameter server param_server_ = param_server(W1, b1, W2, b2, y) node1 = node(W1, b1, W2, b2, param_server_, "node1") node2 = node(W1, b1, W2, b2, param_server_, "node2") nodes = []; nodes.append(node1) nodes.append(node2) num_nodes = 2 # Create threads to execute the backward and forward pass for each node on a different thread jobs = [] jobs.append(threading.Thread(target=forward_and_backward_pass)) jobs.append(threading.Thread(target=forward_and_backward_pass)) for j in jobs: j.setDaemon(True) j.start() execution_time = 0 use_threading = 0 for i in range(12000): # Create a random shuffling of the data. Karpathy's original code uses the same data in each iteration. In a real # world application, each mini-batch will consist of a random shuffling (without replacement) of the training data # One pass over the entire training data is called an "Epoch". My implementation is somewhere in the middle, where # the entire training data is used in each training iteration, but each node gets a random shuffling of the data # and thus operates on a different set of data every iteration. idx = 0 random_inds = np.random.permutation(np.arange(0, num_examples)) X = X[random_inds, :] y = y[random_inds] # Send data to each node. On a real system, our training data will be stored in the main memory. A random "minibatch" # will be sampled from the training data and sent over to the GPUs (usually over a PCIe connection, which can become # a bottleneck when a minibatch consists of a large amount of data such as image data). for node in nodes: node.data(X[idx:B + idx, :], y[idx:B + idx]) idx += B t0 = time.time() if (use_threading): for node_idx in range(0, 2): task_queue.put(nodes[node_idx]) # Wait for the threads to finish. After executing its backward pass, each node will send its computed # gradients to the parameter server. When the parameter server has received gradients from all nodes, it will # compute the updated weights and send them back to each node task_queue.join() else: for node_idx in range(0,2): nodes[node_idx].forward_and_backward() t1 = time.time() execution_time += t1 - t0 # evaluate accuracy. In a real system, the accuracy will be determined on a separate set of training data that was # not used for training. We don't do that in this toy example. scores = node1.l2_o predicted_class = np.argmax(scores, axis=1) print('training time: %.2f' % execution_time) print('training accuracy: %.2f' % (np.mean(predicted_class == y[0:B]))) |

I was wondering if you would need a lock around the param server object?
That’s a good point! Probably.. although even if the updates from one thread are interrupted by another, the average shouldn’t change, because it doesn’t matter which order the gradients are accumulated. However there could be some other race condition going on, so putting a lock around the update_weights function is a good idea.